Rompicapi | Alcuino di York | Un padre di famiglia

«Solo perché un problema non è ancora stato risolto non è detto che sia impossibile da risolvere.» Agatha Christie

Oggi ragioneremo insieme su un rompicapo descritto all’interno del testo di Raffaella Franci in cui ripropone diversi giochi matematici ideati da Alcuino di York. Monaco inglese, chiamato alla corte di Carlomagno nell’anno 781, raccolse questi giochi matematici in una serie di problemi originali da usare per educare i giovani.

 

Alcuino di York

«Dietro ogni problema c’è un’opportunità.» Galileo Galilei

 

Alcuino di York (735 – 804 d.C.) studiò, appunto, nella scuola di York (Inghilterra del Nord), uno delle più rinomate dell’epoca di cui, tra l’altro, divenne direttore.

Nel 781 d.C. giunse alla corte di Carlomagno per dirigere la Schola Palatina (scuola di palazzo) e, successivamente, incaricato di organizzare l’istruzione di tutto il regno.

Dal punto di vista dell’organizzazione degli studi, era convinto sostenitore delle sette arti liberali: grammatica, retorica e logica (trivium), aritmetica, geometria, astronomia e musica (quadrivium). Scrisse molti testi didattici ma sfortunatamente solo Le Propositiones ci è pervenuto. È il più antico testo matematico medievale. Si tratta di una collezione di 53 problemi la cui maggioranza appartiene al genere conosciuto come matematica ricreativa.

Ecco un breve video sulla Rivoluzione Culturale attuata da Alcuino di York.

 

 

In precedenza avevamo pubblicato un articolo su un altro rompicapo di Alcuino di York. Per chi se lo fosse perso, può guardarlo al seguente collegamento ipertestuale: rompicapo del lupo, della capra e del cavolo.

Che cos’è un gioco matematico?

«Sprigionare l’atomo non ha creato un nuovo problema. Ha semplicemente reso più urgente la necessità di risolverne uno esistente.» Albert Einstein

 

Il gioco matematico è un quesito che esclude il ricorso a un vocabolario matematico e la cui soluzione richiede strumenti matematici elementari. Inoltre il suo enunciato deve essere intrigante per chi lo legge e presentare una sfida, deve stimolare la voglia di risolverlo.

Da circa 4000 anni i giochi matematici costituiscono sia un passatempo sia una parte integrante dell’educazione matematica. Anticamente la matematica veniva trasmessa tramandando una raccolta di problemi, spesso raggruppati in base ai metodi risolutivi.

Alcuni autori giustificano la presenza di giochi matematici all’interno di queste raccolte proprio con l’intento di distrarre i lettori dalle noiose teorie matematiche attirandoli con applicazioni pratiche e divertenti.

 

Rompicapo odierno: “Un padre di famiglia”[1].

«La maggioranza dei problemi non deriva dalle risposte che ci diamo ma dalle domande che ci poniamo.» Giorgio Nardone

 

«Un padre di famiglia ordinò di portare 90 moggia[2]  di grano da una sua casa ad un’altra che era distante 30 leghe[3], in modo che un cammello portasse tutto quel frumento in tre viaggi, e in ogni viaggio portasse 30 moggia, il cammello invero per ogni lega mangiava un moggio. Dica, chi vuole, quanti furono i moggi rimasti.»

A mio avviso questo problema è uno tra i più interessanti della raccolta proposta da Alcuino di York. In sintesi, un cammello deve trasportare 90 moggia di grano da una casa ad un’altra distante tra loro 30 leghe. Il cammello però non può trasportare più di 30 moggia per volta e mangia, quando è carico, un moggio di grano per ogni lega percorsa. Il quesito chiede di quantificare il grano che può essere effettivamente trasferito.

 

 

Rompicapo | Soluzione di getto

«Un giorno le macchine riusciranno a risolvere tutti i problemi, ma mai nessuna di esse potrà porne uno.» Albert Einstein

 

Di primo acchito, verrebbe da dire che nessuna moggia di grano giungerà nella seconda casa visto che il cammello, dovendo fare 3 viaggi di 30 leghe ciascuno, mangerà tutte le 90 moggia di grano. Siamo sicuri che non ci sono altre possibili soluzioni?

 

 

 

Rompicapo | Siamo sicuri non ci siano altre soluzioni?

«Ogni problema ha tre soluzioni: la mia soluzione, la tua soluzione e la soluzione giusta.» Platone

 

 

Rompicapo | Prima Soluzione

Nel primo trasporto il cammello portò 30 moggia per 20 leghe. Mangiando un moggio per ogni lega, significa che mangiò 20 moggia e che ne lasciò 10.

Nel secondo trasporto analogamente portò altre 30 moggia per 20 leghe mangiandone 20 e, di conseguenza, lasciandone altre 10.

Nel terzo trasporto fece lo stesso. 30 moggia trasportate, mangiate 20 e rimaste 10. Si tenga a mente che, in questa fermata intermedia distante 20 leghe dalla partenza, rimasero 30 moggia con 10 leghe di viaggio ancora da coprire. Proseguendo quindi nel suo terzo viaggio (Alcuino lo ha chiamato quarto viaggio probabilmente per differenziarlo dai prime 3), il cammello arrivò alla casa di destinazione, mangiando 10 moggia durante quest’ultimo tratto di viaggio. Giunsero quindi a destinazione 20 moggia del carico originario.

Questa è la soluzione presentata da Alcuino in quanto il cammello compie effettivamente 3 viaggi, i primi due di lunghezza pari a 20 leghe mentre, l’ultimo, da 30 leghe con una fermata intermedia.

Altra osservazione da fare è che l’autore, nella soluzione suggerita, indica implicitamente che il cammello mangia solo quando è carico.

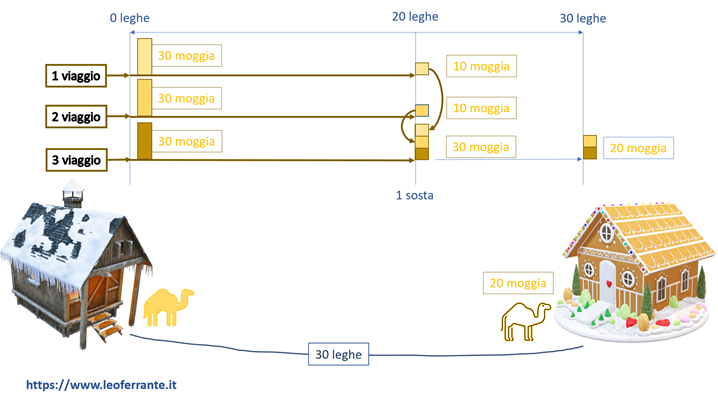
La straordinarietà di questo problema risiede proprio nella sua definizione che, ad una prima analisi, indurrebbe a concludere che nessuna moggia giungerà alla seconda casa. Solo l’accorgimento di costituire un deposito intermedio lungo il percorso (in questo caso a due terzi del percorso) consente al lettore arguto di individuare un’altra soluzione in grado di portare a destinazione 20 moggia di grano.

 

Rompicapo | Seconda soluzione

Cosa accadrebbe se si creasse più di un deposito intermedio? Riusciremmo magari a portare a destinazione più di 20 moggia di grano nella seconda casa? Come?

 

L’idea che soggiace dietro questa seconda possibile soluzione è quella di creare due depositi intermedi lungo il percorso a distanze diverse.

Nel 1 viaggio il cammello si ferma a 10 leghe di distanza dalla partenza, lasciando in questa prima sosta intermedia 20 moggia.

Nel 2 viaggio il cammello giunge a 10 leghe di distanza (primo punto di sosta intermedia) con 20 moggia ancora a bordo. Carica 10 delle 20 moggia dalla sosta intermedia, riportando il proprio carico a 30 moggia. A questo punto prosegue il suo secondo viaggio fino a 25 leghe dalla partenza ovvero 15 leghe ulteriori dopo la sosta intermedia. A questo punto si troverà a 25 leghe di distanza dalla partenza e depositerà le rimanenti 15 moggia di grano (seconda sosta intermedia).

Nel 3 viaggio il cammello giunge alla distanza di 10 leghe con 20 moggia di grano residui. Carica i 10 moggia residui dalla prima sosta intermedia portando il proprio carico a 30 moggia. Muove di ulteriori 15 leghe giungendo alla seconda sosta intermedia dove avrà 15 moggia residui. Caricherà le 15 moggia accantonati presso questo punto proseguendo per ulteriori 5 leghe per giungere alla seconda casa con 25 moggia residui.

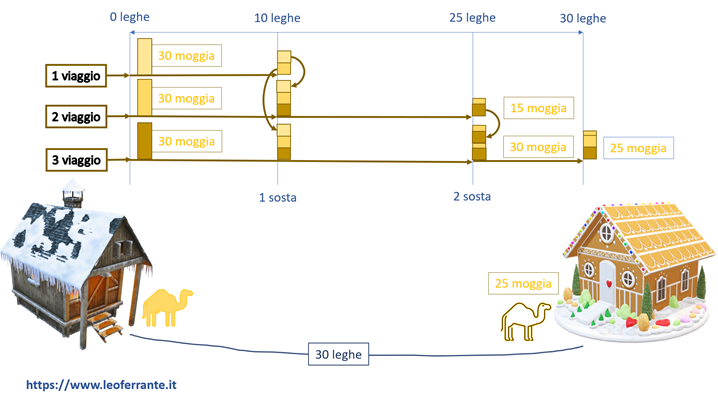
Ecco trovata un’altra soluzione … che tra l’altro renderebbe ancor più felice il padre di famiglia!

Avete altre possibili soluzioni da suggerire?

 

Rompicapo | Possibili applicazioni pratiche di questo tipo di problemi?

«L’uomo è l’unico animale la cui esistenza è un problema che deve risolvere.» Erich Fromm

 

Problemi di questo tipo nascono naturalmente nell’ambito dell’organizzazione di spedizioni in zone prive di supporti logistici e sono attualmente molto importanti nella preparazione dei viaggi spaziali.

 

 

[1] Alcuino di York (a cura di Raffaella Franci), Giochi matematici alla corte di Carlomagno. Problemi per rendere acuta la mente dei giovani, EDIZIONI ETS, Pisa, 2005, pagg. 118 e 119.

[2] mòggio: s. m. [lat. mŏdius, prob. der. di modus «misura»; cfr. modio] (pl. le mòggia, meno comune i mòggi, antico le mògge). – 1. a. Antica unità di misura di capacità per aridi, soprattutto per le granaglie.

[3] La lega era un’unità di lunghezza, variante da luogo a luogo, ed esprimeva originariamente la distanza che una persona, o un cavallo, poteva percorrere al passo in un’ora di tempo (a seconda dei luoghi una grandezza variabile tra i 4 e i 6 chilometri).