Cari lettori, a grande richiesta, pubblico il mio secondo articolo dedicato ai “problemi per acuire la mente”. Lo dividerò in due parti: nella prima mostrerò le soluzioni ai due rompicapi presentati nel precedente articolo mentre, nella seconda parte, presenterò il “dilemma della candela“.
Per chi non lo avesse fatto consiglio di leggere prima il precedente articolo intitolato “Pensiero laterale e pensiero verticale: due modi tra loro complementari”. Questo è necessario onde evitare di leggere soluzioni a problemi che si disconoscono.

RISPOSTA AL PROBLEMA DELLA CAPRA, DEL CAVOLO E DEL LUPO
Questo è un tipico problema di pensiero verticale, risolvibile avvalendosi della logica e servendosi prevalentemente dell’emisfero sinistro del nostro cervello. Il problema ammette le seguenti due possibili soluzioni:
- l’uomo dovrà spostarsi con la sua barchetta per 3 volte: inizierà col traghettare la capra nell’altra riva lasciandola lì sola (1° viaggio), proseguirà tornando da solo indietro (2° viaggio), caricherà il lupo e il cavolo e si sposterà sull’altra con loro (3° viaggio). Il gioco è fatto.
- la seconda soluzione è simile alla prima. Occorre però invertire la sequenza dei trasportati. Nel primo traghettamento porterà nell’altra riva il lupo e il cavolo (1° viaggio), proseguirà tornando indietro solo (2° viaggio), caricherà la capra ricongiungendosi, sull’altra riva, con il lupo e il cavolo (3° viaggio). Il problema è così risolto.

È possibile imbattersi in altre varianti di questo rompicapo. In alcuni testi ho trovato problemi analoghi che davano la possibilità di poter trasportare sulla barca unicamente il cavolo o il lupo o la capra. La logica che guiderà la risoluzione di questo problema declinato diversamente sarà la medesima, seppur contemplando qualche viaggio in più.
“Da Aristotele in poi, la logica viene esaltata come l’unico strumento in grado di trar buon frutto dall’intelletto. Ciononostante, l’imprevedibilità stessa delle idee nuove sta ad indicare che esse non sono necessariamente il risultato di ragionamenti logici.” Edward De Bono
Il problema della capra, del lupo e del cavolo ebbe grande diffusione nel Medioevo ma, recentemente, alcuni studiosi hanno scoperto che questo rompicapo è noto anche in diverse parti dell’Africa. In questo caso, i protagonisti sono ovviamente diversi e in armonia con il proprio habitat. In Liberia, ad esempio, vi sono un pollo, un ghepardo e del riso mentre, in Algeria, una capra, uno sciacallo e un fascio di fieno. Dagli approfondimenti condotti non si è riusciti a stabilire quale sia la versione più antica fra quelle africane ed europea[1].
POSSIBILI RISPOSTE AL PROBLEMA DEI “9 PUNTI”
Il problema dei “9 PUNTI” ammette diverse soluzioni. Per trovarle è necessario sfruttare l’emisfero destro del nostro cervello, facendo ampio ricorso al pensiero laterale. Alla base di questi problemi vi è l’esistenza di un cliché, di un luogo comune, di un modo stereotipato di descrivere o considerare qualcosa. Sovente, nel risolverli, siamo soliti assegnarci più vincoli di quelli che effettivamente ci sono. La maggior parte di coloro che si cimenta, per la prima volta, nella risoluzione di questo rompicapo si ‘auto vincola’, convincendosi di non poter uscire dai confini immaginari ottenuti unendo gli 8 punti più esterni. Ciò accade molto più spesso di quanto si possa pensare anche nella quotidianità[2].

“Un giorno Cristoforo Colombo chiese ai suoi amici se fossero in grado di far stare un uovo dritto su una delle due punte. Gli amici provarono ma il tentativo fallì. Allora Colombo prese un uovo, ne schiacciò una punta e su questa lo fece star ritto. Gli amici protestarono dicendo che per essi valeva la condizione che l’uovo dovesse restare intatto. Cioè essi ponevano dei limiti che in realtà non esistevano. Quante volte tu fai la stessa cosa nelle sfide di ogni giorno?” Edward De Bono
Mostrerò alcune possibili soluzioni al problema dei “9 PUNTI”. Questo proprio a dimostrazione delle enormi potenzialità offerte dal pensiero laterale, soprattutto quando ci troviamo a dover risolvere problemi che ammettono più di una soluzione[3].
Teniamo bene a mente che l’enunciazione di un problema implica la determinazione dei veri confini del problema stesso. Il problema dei “9 PUNTI” prevede di unire tutti i nove punti tracciando il minor numero di linee rette possibile e senza mai staccare la matita dal foglio.
La soluzione ovvia ed immediata che sarà venuta in mente a molti è quella che prevede l’utilizzo di 5 linee. Qui si fa ricorso al solo pensiero verticale, lasciandosi guidare dalla logica e dalla razionalità.
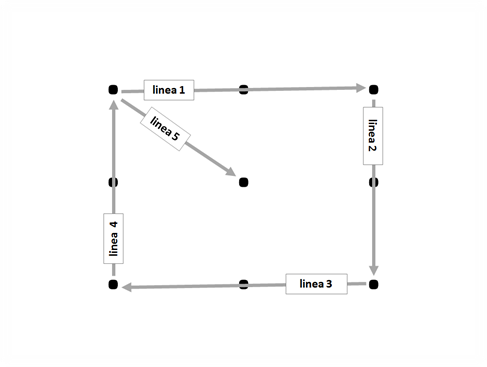
Appena iniziamo a fare ricorso al pensiero laterale, ci spostiamo al di fuori del perimetro della figura. In tal modo riusciamo a risolvere il problema con 4 linee. Ciò è possibile proprio perché, nell’enunciazione del problema da risolvere, non è preclusa la possibilità di andare anche oltre il confine immaginario della figura formatasi unendo gli 8 punti esterni.
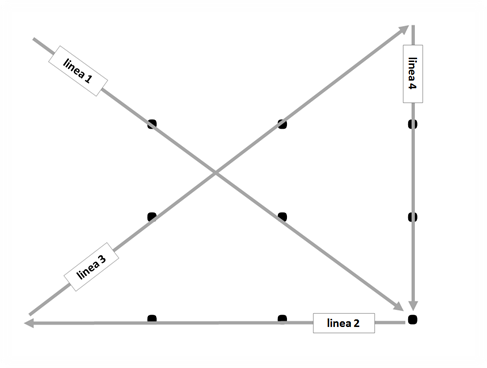
Altro vincolo che solitamente ci imponiamo è quello di rimanere nelle due dimensioni. Perché non esplorare cosa succede andando a ragionare nelle tre dimensioni? Cosa succederebbe se piegassimo il foglio in più parti? Riusciremmo forse ad unire i 9 punti con una sola linea? Vediamo se è possibile:
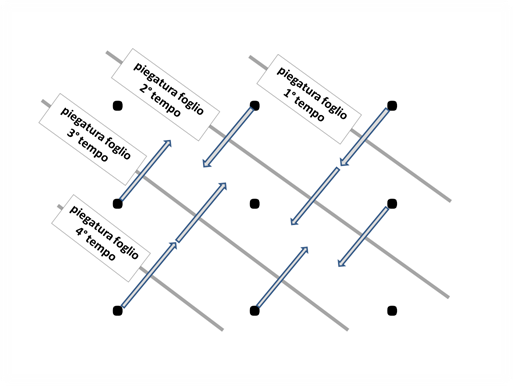
5° ed ultimo tempo
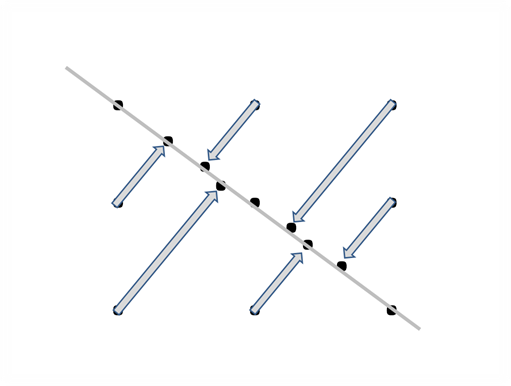

E il gioco è fatto … con una sola linea!
Una bambina di 10 anni, posta dinanzi al medesimo problema, propone di usare una sola linea di spessore pari alla distanza che intercorre tra 3 puntini per racchiuderli tutti in questa macro-linea[4]. Se ci pensiamo bene, nella definizione del problema c’era per caso qualche vincolo che facesse esplicito riferimento allo spessore delle linee da usare?
Da queste prime soluzioni ci siamo subito accorti che il problema analizzato offre svariate altre possibili soluzioni che qui non sono state presentate per evitare inutili appesantimenti. Lascio a te lettore qualche altro spunto di riflessione per esplorare altre possibili soluzioni.
E se magari fosse possibile piegare il foglio in tante parti in modo da far trovare i “9 PUNTI” sovrapposti? In tal modo sarebbe forse possibile unirli con uno spillo? Che ne dite?
E se invece, si arrotolasse il foglio di carta avvolgendo una bottiglia o una lattina, avendo cura di creare un disallineamento nel momento in cui andiamo a far combaciare i due lati lunghi del foglio di carta? Così facendo ci consentirebbe di unire i 9 punti con una sola linea che ruota tutto intorno alla bottiglia?
“È una caratteristica delle soluzioni intuitive e delle nuove idee quella di essere ovvie una volta che sono state scoperte.” Edward De Bono
Siamo adesso tutti più consapevoli di quanto sia dirompente il pensiero laterale nella risoluzione di problemi che, ovviamente, ammettono più soluzioni.
IL DILEMMA DELLA CANDELA
Ora voglio presentarvi il dilemma della candela, nato dall’esperimento condotto nel 1945 da Karl Duncker, uno psicologo tedesco. I materiali necessari sono: una candela, una scatola di chiodi e una confezione di fiammiferi. Il problema da risolvere invece è il seguente: «come attacchereste la candela al muro?».

COSA NON FARE
Permettetevi di darvi un consiglio: resistete alla naturale tentazione di googlare per cercare la soluzione al problema. Lasciate pensare il vostro emisfero destro e sforzatevi di individuare possibili soluzioni. Quando non abbiamo fretta, come in questo caso, utilizziamo il nostro meraviglioso cervello preferendolo alla risposta immediata fornita da un’intelligenza artificiale (l’algoritmo di Google). Ogni volta che cediamo a questa tentazione percorrendo la via più semplice, rendiamo il nostro cervello più pigro e meno elastico. Viceversa, quando optiamo per il suo impiego, evitiamo di sotto impiegarlo rendendolo meno pigro e più elastico.
“La creatività è senza dubbio la risorsa umana più importante. Senza creatività non ci sarebbe progresso e ripeteremmo sempre gli stessi schemi.” Edward De Bono
Delle possibili soluzioni di quest’ultimo dilemma discuteremo nel prossimo articolo che pubblicherò nella categoria “Problemi per acuire la mente”.
Se volete, commentate e inviatemi via posta elettronica le vostre soluzioni. Sarà l’occasione di arricchirsi vicendevolmente.
Non vedo l’ora di leggere le vostre soluzioni e ricevere i vostri commenti!
A presto!
[1] Alcuino di York (a cura di Raffaella Franci), Giochi matematici alla corte di Carlomagno. Problemi per rendere acuta la mente dei giovani, EDIZIONI ETS, Pisa, 2005, pag. 55.
[2] Edward De Bono, Creatività e pensiero laterale, BUR Rizzoli, Milano, 2014, pp. 89 – 95
[3] Leo Ferrante, Innovazione e creatività: quale modello organizzativo e stile di leadership adottare? Proposta di applicazione all’interno del sistema di informazione per la sicurezza della repubblica, Casa Editrice Il Filo di Arianna, La Spezia, 2020, pp. 118 – 123.
[4] Murray Gell-Mann, Il quark e il giaguaro. Avventura nel semplice e nel complesso, Bollati Boringhieri, Torino, 2017, pp. 308-309.

1a sol) Un bel chiodo nello stoppino… 😉
2a sol) Metto la candela a terra attaccato al muro
Buonasera Max,
grazie per le soluzioni suggerite.
Torneremo a parlarne nelle prossime settimane.
Un caro saluto,
Leo
Accendo la candela col fiammifero, aspetto che si scioglie tutta poi modello la cera ancora calda in modo da farla diventare una sorta di foglio, che una volta freddato fisso al muro con uno dei chiodi.
Buonasera Marica e grazie per aver condiviso con noi la sua idea.
Nelle prossime settimane torneremo a parlare delle possibili soluzioni a questo dilemma.
La aspetto sul blog.
Ne approfitto per augurarle una buona serata!
Leo
Ciao, Accendo candela e colo una parte della cera nella scatola svuotata dei chiodi in modo opportuno a garantire comunque equilibrio.
Avvicino la scatola con la candela in equilibrio al muro e la fisso con alcuni chiodi al muro. In caro saluto
Andrea buon pomeriggio,
grazie per aver condiviso la tua soluzione.
Torneremo a parlare del dilemma tutti insieme tra qualche settimana.
Un caro saluto,
Leo
come attacchereste la candela al muro?
1) Accenderei la candela con i fiammiferi
2) metterei la cera che cola sulla testa dei chiodi e li attaccherei al muro con la punta verso l’esterno
3) avrei creato una superficie sul muro pungente dove agganciare la mia candela
Grazie per aver commentato Gianluca.
Cerchiamone altre.
Tra qualche settimana metteremo insieme tutti i commenti ricevuti e ne discuteremo insieme.
Un caro saluto,
Leo